Der Goldene Schnitt ist ein althergebrachter Fachbegriff für das Teilungsverhältnis von Strecken, Flächen oder Körpern. Oft werden Flächen in der Kunst oder in der Fotografie im Goldenen Schnitt geteilt.
Der Sachverhalt, der heute mit „Goldener Schnitt“ bezeichnet wird, ist vermutlich seit mehreren tausend Jahren bekannt. Am Parthenon in Athen, erbaut um 450 vor Christus, kann der Goldene Schnitt an mehreren Fassaden gefunden werden. Im Jahr 300 vor Christus hat Euklid den Goldenen Schnitt in einem seiner Werke erwähnt.
Werden Längen, Flächen oder Körper im Goldenen Schnitt geteilt, so empfindet dies die weit überwiegende Mehrheit der Menschen nachweislich als harmonisch.
Berechnung
Wird eine Fläche im Goldenen Schnitt geteilt, dann gelten folgende Bedingungen:
|
|
Das bedeutet,
- die größere Teilfläche ist ungefähr 1,618-mal so groß wie die kleinere Teilfläche
und gleichzeitig - die Gesamtfläche ist ungefähr 1,618-mal so groß wie die größere Teilfläche.
Der Kehrwert ist genau um 1 kleiner.
| b | = | c | = | 1 | = | 0,618 |
| a | b | 1,618 |
Da 0,618 ungefähr 2/3 ist, findet man oft auch die einfache Drittelung von Seiten als Annäherung an den Goldenen Schnitt. Dies wird aber bereits als deutlich weniger harmonisch empfunden, obwohl der Unterschied zwischen Drittelung und Goldenem Schnitt nur klein ist.
| Teilfläche b | Gesamtfläche a |
| Teilfläche c |
Seitenaufbau mit dem Goldenen Schnitt
In der Typografie wird empfohlen, den Satz einer Seite im Goldenen Schnitt anzulegen. Da es dabei um ein harmonisches Verhältnis von bedruckter Fläche zu weißer Fläche geht, ist es naheliegend, die Regeln des Goldenen Schnitts anzuwenden.
Fibonacci-Reihe
Der Goldene Schnitt weist einige mathematische Besonderheiten auf, die auf den ersten Blick sehr erstaunlich sind.
Erstaunlich ist schon die Tatsache, dass der Kehrwert genau um 1 kleiner ist. Doch noch erstaunlicher ist aber sicherlich die Tatsache, dass sich die Quotienten der Elemente einer Fibonacci-Reihe dem Goldenen Schnitt nähern.
In einer Fibonacci-Reihe wird jede nachfolgende Zahl der Reihe aus der Summe der beiden vorhergehenden Zahlen gebildet.
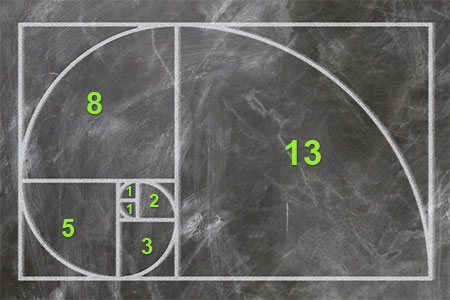
1 1 2 3 5 8 13 21 34
Eine Fibonacci-Reihe gibt zum Beispiel die Kantenlängen der Quadrate in der nachfolgenden Illustration an.
Interessant in diesem Zusammenhang ist sicher auch, dass man die entstandene Kurve auch im Tierreich wiederfindet, zum Beispiel beim Wachstum der ausgestorbenen Ammoniten oder bei Schnecken.
Je größer die Fibonacci-Zahlen werden, desto näher liegt der Quotient zweier Nachbarzahlen am Goldenen Schnitt. Dabei schwingen die Ergebnisse um den Goldenen Schnitt herum und sind abwechselnd größer und kleiner als 1,618.
| 1 / 1 | = | 1 | < | 1,618 |
| 2 / 1 | = | 2 | > | 1,618 |
| 3 / 2 | = | 1,5 | < | 1,618 |
| 5 / 3 | = | 1,67 | > | 1,618 |
| 8 / 5 | = | 1,6 | < | 1,618 |
| 13 / 8 | = | 1,625 | > | 1,618 |
| 21 / 13 | = | 1,615 | < | 1,618 |
| 34 / 21 | = | 1,619 | > | 1,618 |
Fragen des Autors an die Leser
Gestaltungen, die den Goldenen Schnitt berücksichtigen, werden von der Mehrheit der Menschen als harmonisch empfunden. Warum eigentlich? Vielleicht wissen unsere Leser darüber mehr.
Vielleicht gibt es auch mathematisch interessierte Leser, die den Zusammenhang zwischen der Fibonacci-Reihe und dem Goldenen Schnitt erklären können. Gibt es dafür überhaupt eine wissenschaftliche Erklärung?
Und gibt es weitere Brüche (Verhältniszahlen), deren Differenz mit dem Kehrwert genau eine ganze Zahl ergibt, oder ist das ein seltener Zufall?



Hinterlasse einen Kommentar